Phương pháp giải:

Thể tích khối hộp \(V=Sh\)với Slà diện tích đáy và h là chiều cao.

Sử dụng phương pháp cộng, trừ thể tích các khối đa diện.

Lời giải chi tiết:

Ta có: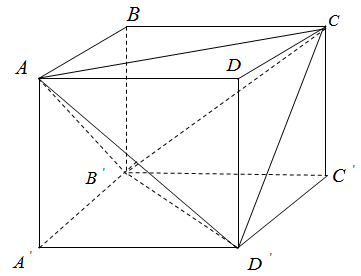

\({{V}_{ACB'D'}}={{V}_{ABCD.A'B'C'D'}}-{{V}_{A.A'B'D'}}-{{V}_{D.ACD'}}-{{V}_{C.B'C'D'}}-{{V}_{B'.ABC}}\)

Mà \({{V}_{A.A'B'D'}}=\frac{1}{3}{{S}_{A'B'D'}}.h=\frac{1}{3}.\frac{1}{2}{{S}_{A'B'C'D'}}.h=\frac{1}{6}{{S}_{A'B'C'D'}}.h=\frac{1}{6}{{V}_{ABCD.A'B'C'D'}}\)

\(\Rightarrow {{V}_{A.A'B'D'}}={{V}_{D.ACD'}}={{V}_{C.B'C'D'}}={{V}_{B'.ABC}}=\frac{1}{6}{{V}_{ABCD.A'B'C'D'}}\)

\(\begin{array}{l} \Rightarrow {V_{ACB'D'}} = {V_{ABCD.A'B'C'D'}} - 4.\frac{1}{6}{V_{ABCD.A'B'C'D'}} = \frac{1}{3}{V_{ABCD.A'B'C'D'}}\\ \Rightarrow \frac{{{V_{ACB'D'}}}}{{{V_{ABCD.A'B'C'D'}}}} = \frac{1}{3}\end{array}\) 

Đáp án B