Câu hỏi
Hàm số \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\left( a\ne 0 \right)\) có bảng biến thiên sau:
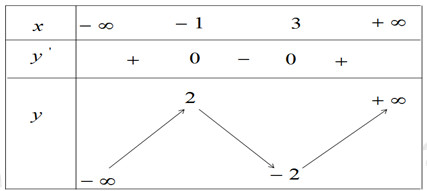
Xác định dấu của a và d ?
- A \(a>0,d<0\)
- B \(a<0,d=0\)
- C \(a<0,d>0\)
- D \(a>0,d>0\)
Phương pháp giải:
Quan sát bảng biến thiên và nhận xét dấu của \(a\), điểm cực đại, cực tiểu để rút ra kết luận.
Lời giải chi tiết:
\(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\Rightarrow y'=3a{{x}^{2}}+2bx+c\)
Từ bảng biến thiên của đồ thị hàm số ta thấy hàm số đạt cực trị tại\(x=-1\)và \(x=3.\)
Do đó \(y'=3a{{x}^{2}}+2bx+c=3a\left( x+1 \right)\left( x-3 \right)\)
\(\Leftrightarrow 3a{{x}^{2}}+2bx+x=3a{{x}^{2}}-6ax-9a\)
\(\Rightarrow b=-3a\) và \(c=-9a.\)
Tại \(x=-1\)thì \(y=2\) cho nên \(\Rightarrow -a+b-c+d=2\Leftrightarrow 5a+d=2\) (1)
Tại \(x=3\) thì \(y=-2\) cho nên \(\Rightarrow 27a+9b+3c+d=-2\Leftrightarrow -27a+d=-2\) (2)
Giải hệ phương trình (1) và (2) ta thu được nghiệm a > 0 và d > 0.
Đáp án D







