Câu hỏi
Đồ thị sau đây là của hàm số nào?
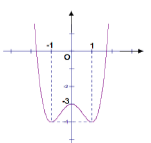
- A \(y={{x}^{4}}-2{{x}^{2}}-3\)
- B \(y=-\frac{1}{4}{{x}^{4}}+3{{x}^{2}}-3\)
- C \(y={{x}^{4}}-3{{x}^{2}}-3\)
- D \(y={{x}^{4}}+2{{x}^{2}}-3\)
Phương pháp giải:
Quan sát đồ thị và tìm các điểm cực trị, đối chiếu với các đáp án bài cho.
Lời giải chi tiết:
Từ đồ thị của hàm số ta dễ dàng thấy được:
Điểm cực tiểu \(\left( -1;-4 \right),\left( 1;-4 \right)\) và điểm cực đại \(\left( 0;-3 \right)\)
Xét Đáp án A: \(y'=4{{x}^{3}}-4x=4x\left( {{x}^{2}}-1 \right)\) có các nghiệm \(x=0;x=\pm 1\).
Do đó đồ thị có các điểm cực tiểu là \(\left( -1;-4 \right),\left( 1;-4 \right)\) và điểm cực đại là \(\left( 0;-3 \right)\).
Đáp án là A







