Phương pháp giải:

Công thức tính thể tích khối chóp \(V=\frac{1}{3}S.h\).

Công thức tính diện tích hình thoi \(S=\frac{1}{2}{{d}_{1}}{{d}_{2}}\) với \({{d}_{1}},{{d}_{2}}\) là hai đường chéo của hình thoi.

Lời giải chi tiết:

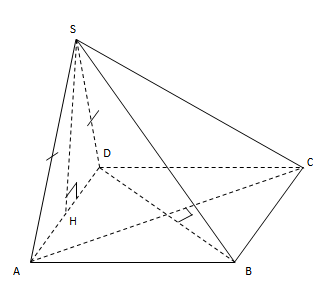
\({{V}_{S.ABCD}}=\frac{1}{3}.{{S}_{ABCD}}SH\)

Với H là chân đường cao kẻ từ S đến mặt phẳng (ABCD).

Khi đó \({{V}_{S.ABCD}}=\frac{1}{3}{{S}_{ABCD}}.SH\) (1)

\({{S}_{ABCD}}=\frac{1}{2}AC.BD=\frac{1}{2}.2a.a={{a}^{2}}\) 

Xét tam giác vuông cân SAD có \(SH=\frac{1}{2}AD=\frac{1}{2}\sqrt{A{{O}^{2}}+O{{D}^{2}}}=\frac{1}{2}\sqrt{\frac{{{a}^{2}}}{4}+{{a}^{2}}}=\frac{a\sqrt{5}}{4}\) (2)

Từ (1) và (2) ta được thể tích \({{V}_{S.ABCD}}=\frac{1}{3}.{{a}^{2}}.\frac{a\sqrt{5}}{4}=\frac{{{a}^{3}}\sqrt{5}}{12}\)

 Đáp án D