Câu hỏi
Cho hàm số \(y=f(x)\) có đồ thị như hình bên. Xác định tất cả các giá trị của tham số m để phương trình \(\left| f\left( x \right) \right|=2{{m}^{2}}-m+3\) có 6 nghiệm thực phân biệt.
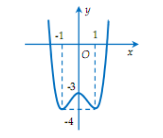
- A \(-\frac{1}{2}<m<0\)
- B \(0<m<\frac{1}{2}\)
- C \(\frac{1}{2}<m<1\)
- D \(\left[ \begin{array}{l}\frac{1}{2} < m < 1\\ - \frac{1}{2} < m < 0\end{array} \right.\)
Phương pháp giải:
- Vẽ đồ thị hàm số \(y=\left| f\left( x \right) \right|\) từ đồ thị hàm số \(y=f\left( x \right)\): giữ nguyên phần đồ thị phía trên trục hoành và lấy đối xứng phần đồ thị phía dưới qua trục hoành.
- Điều kiện để phương trình \(\left| f\left( x \right) \right|=2{{m}^{2}}-m+3\) có 6 nghiệm phân biệt là đường thẳng \(y=2{{m}^{2}}-m+3\) cắt đồ thị hàm số \(y=\left| f\left( x \right) \right|\) tại 6 điểm phân biệt.
Lời giải chi tiết:
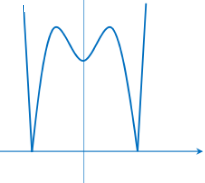
Ta có đồ thị hàm số \(y=\left| f\left( x \right) \right|.\)
Lúc này, để phương trình \(\left| f\left( x \right) \right|=2{{m}^{2}}-m+3\) có 6 nghiệm phân biệt thì đường thẳng \(y=2{{m}^{2}}-m+3\) cắt đồ thị hàm số \(y=\left| f\left( x \right) \right|\) tại 6 điểm phân biệt.
\(\Rightarrow 3<2{{m}^{2}}-m+3<4\) \( \Leftrightarrow \left\{ \begin{array}{l}2{m^2} - m > 0\\2{m^2} - m - 1 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > \frac{1}{2}\\m < 0\end{array} \right.\\-\frac{1}{2} < m < 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\frac{1}{2} < m < 1\\ - \frac{1}{2} < m < 0\end{array} \right.\)
Đáp án D.







