Phương pháp giải:

Phương trình đã cho có nghiệm \(\Leftrightarrow \) đường thẳng \(y=m\) cắt đồ thị hàm số \(y=f\left( x \right)=\sqrt{3+x}+\sqrt{6-x}-\sqrt{\left( 3+x \right)\left( 6-x \right)}\) tại ít nhất 1 điểm nên ta xét hàm \(f\left( x \right)\), từ đó tìm ra điều kiện của \(m\).

Lời giải chi tiết:

Xét hàm số: \(f\left( x \right)=\sqrt{3+x}+\sqrt{6-x}-\sqrt{\left( 3+x \right)\left( 6-x \right)}\)  trên \(\left[ -3;6 \right].\)

\(f'\left( x \right)=0\Leftrightarrow \sqrt{6-x}-\sqrt{3+x}+2x-3=0\) \(\Leftrightarrow \frac{3-2x}{\sqrt{6-x}+\sqrt{3+x}}-\left( 3-2x \right)=0\) \( \Leftrightarrow \left[ \begin{array}{l}x = \frac{3}{2} \in \left[ { - 3;6} \right]\\\sqrt {6 - x}  + \sqrt {3 + x}  = 1(*)\end{array} \right.\)

\((*)\Leftrightarrow 9+2\sqrt{\left( 6-x \right)\left( 3+x \right)}=1\) \(\Leftrightarrow 2\sqrt{\left( 6-x \right)\left( 3+x \right)}=-8\) (loại)

Ta có bảng biến thiên:

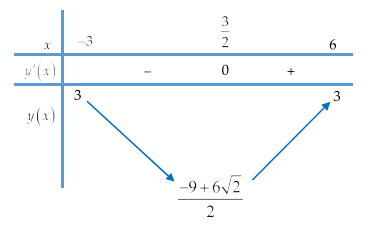
Vậy để phương trình \(f\left( x \right)=m\) có nghiệm thì:\(\frac{-9+6\sqrt{2}}{2}\le m\le 3.\)

Đáp án D.