Phương pháp giải:

Viết phương trình đường thẳng đi qua \(A\) và có hệ số góc \(k\) .

Biện luận số giao điểm của hai đồ thị là số nghiệm của phương trình hoành độ giao điểm để suy ra kết luận.

Lời giải chi tiết:

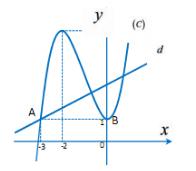
Xét hàm số: \(y={{x}^{3}}+3{{x}^{2}}+1\left( C \right)\)  trên \(R\)

Ta có: \(y'=3{{x}^{2}}+6x\) ; \(y'=0\Leftrightarrow 3{{x}^{2}}+6x=0\)

 \( \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  - 2\end{array} \right.\)

Ta có (C) là hàm số bậc 3 xác định trên \(R\), đồ thị của nó có duy nhất 2 cực trị hoặc không có điểm cực trị nào.

Ta có: \(a=1>0\Rightarrow B\left( 0;1 \right)\) là điểm cực tiểu của (C).

Ta có: \(\overrightarrow{AB}=\left( 3;0 \right)\Rightarrow AB\parallel Ox.\)

\(\Rightarrow \) để thỏa mãn yêu cầu bài toán thì điều kiện cần là k > 0 với k là hệ số góc đường thẳng cắt (C) tại 3 điểm phân biệt.

Gọi \(d:y=kx+a\) với \(k>0;k,a\in R\)

Ta lại có \(A\left( -3;1 \right)\in d\Rightarrow 1=-3k+a\Leftrightarrow a=1+3k.\)

\(\Rightarrow d:y=kx+3k+1.\)

d cắt (C) tại 3 điểm phân biệt \(\Leftrightarrow \) phương trình: \(kx+3k+1={{x}^{3}}+3{{x}^{2}}+1\left( 1 \right)\)  có 3 nghiệm phân biệt.

Phương trình \(\left( 1 \right)\Leftrightarrow \left( x+3 \right)\left( {{x}^{2}}-k \right)=0\)

\( \Leftrightarrow \left[ \begin{array}{l}x =  - 3\\x =  \pm \sqrt k \end{array} \right.\) vì k > 0.

Để phương trình (1) có 3 nghiệm phân biệt \(\Leftrightarrow k\ne 9.\)

Vậy \(k>0;k\ne 9\) thỏa mãn yêu cầu của bài.

Đáp án C.