Phương pháp giải:

- Chứng minh \(\Delta ABC\) vuông tại \(B\), tìm tâm và bán kính đường tròn ngoại tiếp tam giác đáy.

- Sử dụng công thức \({{R}^{2}}=\frac{{{h}^{2}}}{4}+{{r}^{2}}\) với \(R\) là bán kính hình cầu ngoại tiếp khối chóp, \(h\) là chiều cao, \(r\) là bán kính đường tròn ngoại tiếp đa giác đáy.

Lời giải chi tiết:

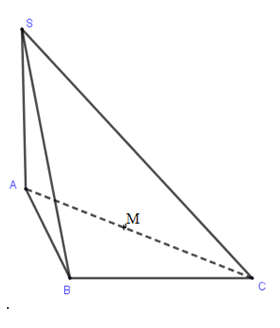
Ta có: \(\cos {{60}^{\circ }}=\frac{1}{2}=\frac{a}{2a}\to \cos \widehat{BAC}=\frac{AB}{AC}\)

\(\Rightarrow \Delta ABC\) vuông tại B.

Gọi M là trung điểm AC.

\(\Rightarrow M\) là tâm đường tròn ngoại tiếp \(\Delta ABC.\)

\(\Rightarrow MA=MC=\frac{AC}{2}=a.\)

Gọi r là bán kính đường tròn ngoại tiếp tam giác đáy.

R là bán kính mặt cầu ngoại tiếp hình chóp.

h là chiều cao hình chóp.

Ta có công thức sau:

\({{R}^{2}}=\frac{{{h}^{2}}}{4}+{{r}^{2}}\Rightarrow{{R}^{2}}=\frac{{{a}^{2}}}{4}+{{a}^{2}}=\frac{a\sqrt{5}}{2}\)

\(\Rightarrow V=\frac{4}{3}\pi {{R}^{3}}=\frac{5{{a}^{3}}\sqrt{5}}{6}.\)

Đáp án B