Câu hỏi
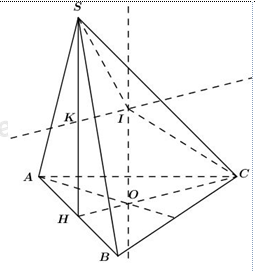
Cho hình chóp S.ABC có đáy là tam giác đều cạnh 1, tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích của khối cầu ngoại tiếp hình chóp đã cho.
- A \(V=\frac{5\sqrt{15}\pi }{54}\)
- B \(V=\frac{5\sqrt{15}\pi }{18}\)
- C \(V=\frac{4\sqrt{3}\pi }{27}\)
- D \(V=\frac{5\pi }{3}\)
Phương pháp giải:
+) Tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy nên \(SH\bot \left( SAB \right)\) với H là trung điểm của AB.
+) Gọi O là tâm đường tròn ngoại tiếp tam giác ABC.
+) Dựng đường thẳng d qua O và vuông góc với (ABC), khi đó d là trục của mặt cầu ngoại tiếp hình chóp SABC.
+) Dựng mặt phẳng trung trực của (SAB), khi đó mặt phẳng này cắt SH tại K.
+) Tính bán kính mặt cầu ngoại tiếp hình chóp bằng định lý Pi-ta-go.
Lời giải chi tiết:
Gọi H là trung điểm của AB. Khi đó \(SH\bot \left( SAB \right).\)
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, dựng đường thẳng d đi qua O và vuông góc với (ABC).
\(\Rightarrow d//SH.\)
Dựng đường trung trực của (SAB), cắt d tại I. Khi đó I là tâm mặt cầu ngoại tiếp hình chóp SABC.
Gọi K là giao điểm của SH và mặt phẳng trung trực của (SAB).
\(\Rightarrow \) IKHO là hình chữ nhật, K là trọng tâm tam giác SAB
Khi đó: \(R=SI=IA=IB=IC\) là bán kính mặt cầu ngoại tiếp hình chóp SABC.
Tam giác ABC đều cạnh 1 nên \(CH=\frac{\sqrt{3}}{2}\Rightarrow OC=\frac{2}{3}CH=\frac{\sqrt{3}}{3}.\)
Tam giác SAB đều cạnh 1 nên \(SH=\frac{\sqrt{3}}{2}\Rightarrow HK=\frac{1}{3}SH=\frac{\sqrt{3}}{6}=IO\)
Xét tam giác IOC vuông tại O ta có: \(IC=\sqrt{O{{I}^{2}}+O{{C}^{2}}}=\sqrt{\frac{3}{36}+\frac{1}{3}}=\sqrt{\frac{5}{12}}=\frac{\sqrt{15}}{6}\)
\(V=\frac{4}{3}\pi {{R}^{3}}=\frac{4}{3}\pi .{{\left( \frac{\sqrt{15}}{5} \right)}^{3}}=\frac{5\pi \sqrt{15}}{54}\)
Chọn A