Phương pháp giải:

- Tính đạo hàm và tìm các điểm mà tại đó đạo hàm bằng \(0\).

- Tính các giá trị của hàm số tại hai đầu mút và tại các nghiệm của đạo hàm.

- Giá trị lớn nhất trong số những giá trị vừa tìm được là GTLN của hàm số trên đoạn \(\left[ a;b \right]\).

Lời giải chi tiết:

Xét hàm số: \(y=x\left( 2-\ln x \right)\) trên \(\left[ 2;3 \right].\)

Có \(y'\left( x \right)=2-\ln x-1=1-\ln x\)

\(y'\left( x \right)=0\Leftrightarrow 1-\ln x=0\Leftrightarrow \ln x=1\Leftrightarrow x=e\in \left[ 2;3 \right].\)

Ta có bảng biến thiên:

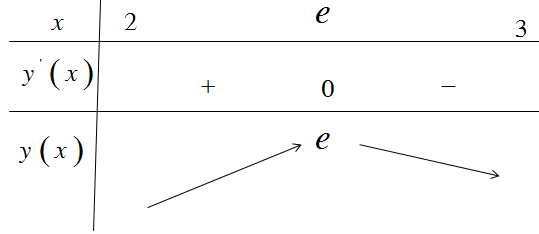
Vậy \(\underset{\left[ 2;3 \right]}{\mathop{\max }}\,y=y\left( e \right)=e.\)

Đáp án C.