Câu hỏi
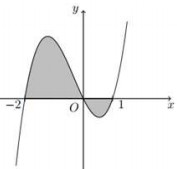
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Diện tích hình phẳng phần tô đậm trong hình vẽ là
- A \(S = \int\limits_{ - \,2}^0 {f\left( x \right){\rm{d}}x} + \int\limits_0^2 {f\left( x \right){\rm{d}}x} .\)
- B \(S = \int\limits_0^{ - \,2} {f\left( x \right){\rm{d}}x} + \int\limits_0^1 {f\left( x \right){\rm{d}}x} .\)
- C \(S = \int\limits_{ - \,2}^0 {f\left( x \right){\rm{d}}x} - \int\limits_0^1 {f\left( x \right){\rm{d}}x} .\)
- D \(S = \int\limits_{ - \,2}^1 {f\left( x \right){\rm{d}}x} .\)
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), x = a, x = b là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \), lưu ý dấu của f(x) trên mỗi đoạn xác định.
Lời giải chi tiết:
Dựa vào hình vẽ, ta thấy trên đoạn \(\left\{ \matrix{ x \in \left[ { - \,2;0} \right]\,\, \Rightarrow \,\,f\left( x \right) \ge 0 \hfill \cr x \in \left[ {0;1} \right]\,\, \Rightarrow f\left( x \right) \le 0 \hfill \cr} \right..\)
Khi đó \(S = \int\limits_{ - \,2}^1 {\left| {f\left( x \right)} \right|{\rm{d}}x} = \int\limits_{ - \,2}^0 {\left| {f\left( x \right)} \right|{\rm{d}}x} + \int\limits_0^1 {\left| {f\left( x \right)} \right|{\rm{d}}x} = \int\limits_{ - \,2}^0 {f\left( x \right){\rm{d}}x} - \int\limits_0^1 {f\left( x \right){\rm{d}}x} .\)
Chọn C.







