Câu hỏi
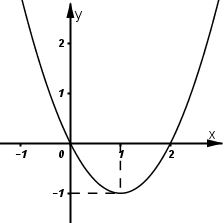
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đạo hàm là hàm số \(y =f’(x)\) có đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số y = f(x) tiếp xúc với trục hoành tại điểm có hoành độ dương. Hỏi đồ thị hàm số y = f(x) cắt trục tung tại điểm có tung độ dương bằng bao nhiêu?
- A \(\dfrac{2}{3}\)
- B \(1\)
- C \(\dfrac{3}{2}\)
- D \(\dfrac{4}{3}\)
Lời giải chi tiết:
\(y = a{x^3} + b{x^2} + cx + d \Rightarrow y' = 3a{x^2} + 2bx + c\left( 1 \right)\)
Có (1) đi qua A(0;0); B(1;-1); C(2;0)
Nên ta có :
\(\left\{ \begin{array}{l}c = 0\\3a + 2b + c = - 1\\12a + 4b + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 0\\a = \frac{1}{3}\\b = - 1\end{array} \right.\)
Khi đó ta có hàm số \(y = \dfrac{1}{3}{x^3} - {x^2} + d;y' = {x^2} - 2x\)
Gọi M(m;0) (m > 0), là điểm tiếp xúc của đồ thị hàm số với trục hoành khi đó ta có:
\(y'\left( m \right) = 0 \Leftrightarrow {m^2} - 2m = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\,\,\,(ktm)\\m = 2\,\,\,(tm)\end{array} \right.\)
Khi đó đồ thị hàm số đi qua điểm M(2;0) nên ta được: \(0 = \dfrac{1}{3}{2^3} - {2^2} + d \Leftrightarrow d = \dfrac{4}{3}\)
Vậy hàm số cắt trục tung tại điểm có tung độ \(\dfrac{4}{3}\).
Chọn đáp án D.







