Câu hỏi
Tìm giá trị lớn nhất của hàm số \(y = {x^3} + 3{x^2} - 9x + 7\) trên đoạn \(\left[ { - 2;\,\,2} \right]\).
- A \(\mathop {\max }\limits_{\left[ { - 2;\,\,2} \right]} y = 9\)
- B \(\mathop {\max }\limits_{\left[ { - 2;\,\,2} \right]} y = 5\)
- C \(\mathop {\max }\limits_{\left[ { - 2;\,\,2} \right]} y = 34\)
- D \(\mathop {\max }\limits_{\left[ { - 2;\,\,2} \right]} y = 29\)
Phương pháp giải:
Sử dụng chức năng [MODE][7] của máy tính CASIO để tìm nhanh giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 2;\,\,2} \right]\).
Lời giải chi tiết:
Ta nhập hàm số f(x) đã cho vào máy tính với Start: -2; End: 2; Step \(\frac{{2 - \left( { - 2} \right)}}{{19}} = \frac{4}{{19}}.\) Ta được:
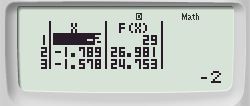
Ta nhận thấy hàm số đạt giá trị lớn nhất bằng 29 tại \(x = - 2.\)
Chọn D.
Câu hỏi trước
