Câu hỏi
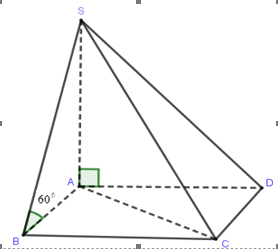
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a,AD = 3a\); hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\), góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABCD} \right)\) bằng \({60^0}\). Khi đó khối chóp \(S.ABC\) có thể tích là:
- A \(\dfrac{{\sqrt 3 {a^3}}}{3}\)
- B \(\dfrac{{\sqrt 3 {a^3}}}{4}\)
- C \(\sqrt 3 {a^3}\)
- D \(\dfrac{{\sqrt 3 {a^3}}}{2}\)
Phương pháp giải:
- Chứng minh \(SA \bot \left( {ABCD} \right)\)bằng cách sử dụng định lý: Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì giao tuyến (nếu có) của chúng vuông góc với mặt phẳng đó.
- Xác định góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABCD} \right)\) bằng cách sử dụng định nghĩa: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng đó và cùng vuông góc với giao tuyến.
- Tính thể tích khối chóp theo công thức \(V = \frac{1}{3}S.h\).
Lời giải chi tiết:
Vì
\(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAC} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {SAC} \right) = SA\end{array} \right.\)
nên \(SA \bot \left( {ABCD} \right)\), do đó \(SA \bot BC\).
Lại có \(AB \bot BC\) nên \(BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\).
Ta có:
\(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\SB \subset \left( {SBC} \right) \bot BC\\AB \subset \left( {ABCD} \right) \bot BC\end{array} \right. \Rightarrow \widehat {SBA} = {60^0}\)
Xét tam giác vuông \(SAB\)có:
\(AB = a,\widehat {SBA} = {60^0} \Rightarrow SA = AB.\tan {60^0} = a\sqrt 3 \)
Vậy thể tích khối chóp \(S.ABC\) là \(V = \frac{1}{3}SA.{S_{ABC}} = \frac{1}{6}SA.AB.BC = \frac{1}{6}.a\sqrt 3 .a.3a = \frac{\sqrt{3}}{2} {a^3}\).
Chọn D.







