Phương pháp giải:

Trải ba mặt bên của hình chóp ra cùng một mặt phẳng. Tìm chu vi của tam giác AB’C’ và tìm SB’, SC’ để chu vi của tam giác AB’C’ là nhỏ nhất.

Lời giải chi tiết:

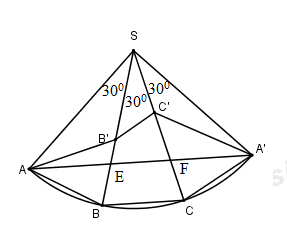
Trải các tam giác SAB, SBC, SAC ra cùng một mặt phẳng \(\left( A'\equiv A \right)\). Ta có \(\Delta SAC=\Delta SA'C\Rightarrow AC'=A'C'\)

Do đó chu vi tam giác AB’C’ là \(AB'+B'C'+C'A=AB'+B'C'+C'A\ge AA'\)

Dấu “=” xảy ra khi \(B'\equiv E,C'\equiv F\) hay \(SB'=SE,SC'=SF.\)

Tam giác SAA’ có góc S = 90⁰, SA = SA’ = a nên tam giác SAA’ vuông cân tại S, do đó \(\widehat{SAA'}=\widehat{SA'A}={{45}^{0}}\).

Xét tam giác SAE có \(\widehat{SEA}={{180}^{0}}-{{30}^{0}}-{{45}^{0}}={{105}^{0}}\). Áp dụng định lí sin ta có:

\(\frac{SE}{\sin \widehat{SAE}}=\frac{SA}{\sin \widehat{SEA}}\Rightarrow \frac{SE}{\sin 45}=\frac{a}{\sin 105}\Rightarrow SE=\left( -1+\sqrt{3} \right)a\)

Hoàn toàn tương tự ta cũng chứng minh được \(SF=\left( -1+\sqrt{3} \right)a\)

Vậy chu vi tam giác AB’C” nhỏ nhất khi và chỉ khi \(SB'=SC'=\left( -1+\sqrt{3} \right)a\)

Khi đó \(\frac{{{V}_{S.AB'C'}}}{{{V}_{S.ABC}}}=\frac{SB'}{SB}.\frac{SC'}{SC}={{\left( -1+\sqrt{3} \right)}^{2}}=4-2\sqrt{3}\Rightarrow k=4-2\sqrt{3}\).

Chọn B.