Câu hỏi
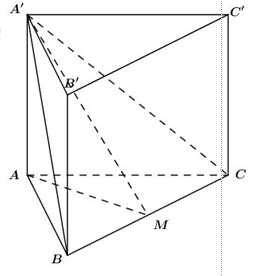
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều. Mặt phẳng (A’BC) tạo với đáy góc \({{30}^{0}}\) và tam giác A’BC có diện tích bằng 8. Tính thể tích V của khối lăng trụ đã cho.
- A \(V=64\sqrt{3}\)
- B \(V=2\sqrt{3}\)
- C \(V=8\sqrt{3}\)
- D \(V=16\sqrt{3}\)
Phương pháp giải:
+) Góc giữa hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) là góc giữa 2 đường thẳng a, b với \(a\in \left( \alpha \right);\,\,\,b\in \left( \beta \right)\) sao cho \(a\bot c;\,\,b\bot c\), c là giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\).
+) Công thức tính thể tích lăng trụ: \(V={{S}_{d}}.h.\)
Lời giải chi tiết:
Gọi M là trung điểm của BC.
Đáy ABC là tam giác đều \(\Rightarrow AM\bot BC\,\,\,\left( 1 \right).\) ABC.A’B’C’ là lăng trụ đứng nên \(\Rightarrow AA'\bot BC\,\,\)
\(\Rightarrow \)\(BC\bot \left( \text{AA}'M \right) \Rightarrow A'M\bot BC\,\,\,\left( 2 \right).\,\)
\(\Rightarrow \) góc giữa (ABC) và (A’BC) là góc giữa A’M và AM
Hay \(\widehat{A'MA}={{30}^{0}}.\)
Gọi độ dài cạnh đáy là a. Khi đó \(AM=\frac{a\sqrt{3}}{2}.\)
Xét tam giác A’AM vuông tại A ta có: \(A'M=\frac{AM}{\cos {{30}^{0}}}=\frac{\frac{a\sqrt{3}}{2}}{\frac{\sqrt{3}}{2}}=a.\)
Khi đó: \({{S}_{A'BC}}=\frac{1}{2}A'M.BC=8\Leftrightarrow \frac{1}{2}.a.a=8\Leftrightarrow {{a}^{2}}=16\Leftrightarrow a=4.\)\(\Rightarrow {{S}_{ABC}}=\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{{{4}^{2}}\sqrt{3}}{4}=4\sqrt{3}.\)
Có \(AA'=AM.\tan {{30}^{0}}=\frac{a\sqrt{3}}{2}.\frac{1}{\sqrt{3}}=\frac{a}{2}=\frac{4}{2}=2.\)\(\Rightarrow {{V}_{ABC.A'B'C'}}=AA'.{{S}_{ABC}}=2.4\sqrt{3}=8\sqrt{3}.\)
Chọn C.