Phương pháp giải:

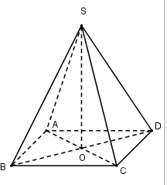
Hình chóp tứ giác đều có chân đường cao là tâm của hình vuông đáy.

Công thức tính thể tích hình chóp:  \(V = {1 \over 3}{S_d}.h.\)

Lời giải chi tiết:

Gọi O là tâm hình vuông ABCD thì \(SO \bot \left( {ABCD} \right)\), khi đó ta có  \(OB = {{BD} \over 2} = {{a\sqrt 2 } \over 2}\)

Xét tam giác vuông SOB có \(SO = \sqrt {S{B^2} - O{B^2}}  = \sqrt {4{a^2} - {{{a^2}} \over 2}}  = {{a\sqrt {14} } \over 2}\)

Vậy \({V_{S.ABCD}} = {1 \over 3}SO.{S_{ABCD}} = {1 \over 3}{{a\sqrt {14} } \over 2}{a^2} = {{{a^3}\sqrt {14} } \over 6}.\)

Chọn D.