Câu hỏi
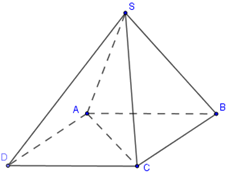
Cho khối chóp S.ABCD có thể tích bằng \(2{{a}^{3}}\) và đáy ABCD là hình bình hành. Biết diện tích tam giác SAB bằng \({{a}^{2}}\) . Tính khoảng cách giữa hai đường thẳng SA và CD.
- A \(\frac{3a}{2}\)
- B 3a
- C 6a
- D a
Phương pháp giải:
Tìm (P) chứa a mà (P) // b. Khi đó d(a, b) = d(b; (P)) = d(I, (P)) với I thuộc b
Lời giải chi tiết:
Ta có (SAB) chứa SA và CD // (SAB)
Nên ta có: d(SA;CD) = d (CD,(SAB)) = d(D;(SAB))
Ta lại có: \(\begin{align}& {{V}_{SABCD}}={{V}_{D.SAB}}+{{V}_{C.SAB}}=2.{{V}_{D.SAB}}=2.\frac{1}{3}{{d}_{\left( D,\left( SAB \right) \right)}}.{{S}_{SAB}} \\& \Rightarrow {{d}_{\left( D,\left( SAB \right) \right)}}=\frac{3V}{2{{S}_{SAB}}}=\frac{3.2{{a}^{3}}}{2{{a}^{2}}}=3a \\\end{align}\)
Chọn B.
Câu hỏi trước
