Phương pháp giải:

Đưa phương trình về dạng \(\ln \left( 1-2x \right)+1-2x=\ln \left( x+y \right)+x+y\), sau đó xét hàm đặc trưng \(f\left( t \right)=\ln t+t\) và chứng minh hàm số \(y=f\left( t \right)\) đơn điệu, suy ra mối quan hệ giữa x và y.

Đưa biểu thức P về một biến x hoặc y, sau đó dùng MTCT để tìm GTNN của P.

Lời giải chi tiết:

ĐK: \(\frac{1-2x}{x+y}>0\), do x, y > 0 nên \(x+y>0\Rightarrow 1-2x>0\Leftrightarrow 0<x<\frac{1}{2};y>0\).

Khi đó ta có:

\(\begin{align}& \,\,\,\,\,\,\,\,\ln \left( \frac{1-2x}{x+y} \right)=3x+y-1\Leftrightarrow \ln \left( 1-2x \right)-\ln \left( x+y \right)=2x+x+y-1 \\& \Leftrightarrow \ln \left( 1-2x \right)+1-2x=\ln \left( x+y\right)+x+y\,\,\,\,\,\,\,\,\,\left( 1 \right) \\\end{align}\)

Xét hàm số đặc trưng \(f\left( t \right)=\ln t+t\) với t > 0 có \(f'\left( t \right)=\frac{1}{t}+1>0\Rightarrow \)Hàm số y = f(t) đồng biến trên \(\left( 0;+\infty  \right)\)

Mà từ (1) ta có \(f\left( 1-2x \right)=f\left( x+y \right)\Rightarrow 1-2x=x+y\Leftrightarrow y=1-3x\)

Khi đó \(P=\frac{1}{x}+\frac{1}{\sqrt{xy}}=\frac{1}{x}+\frac{1}{\sqrt{x\left( 1-3x \right)}},\,\,\,0<x<\frac{1}{2}.\)

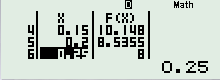
Sử dụng máy tính cầm tay, chức năng [MODE] [7] , ta tìm được \({{P}_{\min }}=8\) khi \(x=\frac{1}{4}\)

Chọn A.