Câu hỏi
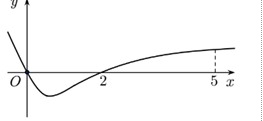
Cho hàm số \(f\left( x \right)\) có đạo hàm trên R và có đồ thị hàm \(y=f'\left( x \right)\) như hình vẽ.
Biết rằng \(f\left( 0 \right)+f\left( 3 \right)=f\left( 2 \right)+f\left( 5 \right).\)
Giá trị nhỏ nhất và giá trị lớn nhất của \(f\left( x \right)\) trên đoạn \(\left[ 0;\,\,5 \right]\) lần lượt là:
- A \(f\left( 2 \right);\,\,f\left( 0 \right)\)
- B \(f\left( 0 \right);\,\,f\left( 5 \right)\)
- C \(f\left( 2 \right);\,\,f\left( 5 \right)\)
- D \(f\left( 1 \right);\,\,f\left( 3 \right)\)
Phương pháp giải:
Dựa vào tính đơn điệu của hàm số, vẽ bảng biến thiên để xác định Min, Max của hàm số f(x).
Lời giải chi tiết:
Từ đồ thị \(y={f}'\left( x \right)\) trên đoạn \(\left[ 0;5 \right],\) ta có \(f'\left( 0 \right)=0;\,\,f'\left( 2 \right)=0\)
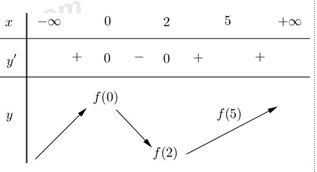
Ta có bảng biến thiên của hàm số \(y=f\left( x \right)\) như hình vẽ bên:
Suy ra \(\underset{\left[ 0;5 \right]}{\mathop{\min }}\,f\left( x \right)=f\left( 2 \right).\) Từ giả thiết, ta có:
\(f\left( 0 \right)+f\left( 3 \right)=f\left( 2 \right)+f\left( 5 \right)\Leftrightarrow f\left( 5 \right)-f\left( 3 \right)=f\left( 0 \right)-f\left( 2 \right)\)
Hàm số \(y=f\left( x \right)\) đồng biến trên \(\left[ 2;5 \right];3\in \left[ 2;5 \right]\Rightarrow f\left( 3 \right)>f\left( 2 \right)\)
\(\Rightarrow f\left( 5 \right)-f\left( 2 \right)>f\left( 5 \right)-f\left( 3 \right)=f\left( 0 \right)-f\left( 2 \right)\Leftrightarrow f\left( 5 \right)>f\left( 0 \right)\)
Suy ra \(\underset{\left[ 0;5 \right]}{\mathop{\max }}\,f\left( x \right)=\left\{ f\left( 0 \right),\,\,f\left( 5 \right) \right\}=f\left( 5 \right).\)
Chọn C.