Câu hỏi
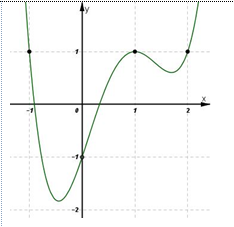
Cho hàm số f(x) xác định trên R và có đồ thị f’(x) như hình vẽ. Đặt g(x) = f(x) – x. Hàm số g(x) đặt cực đại tại điểm nào sau đây?
- A x = 1
- B x = 2
- C x = 0
- D x = - 1
Phương pháp giải:
Hàm số y = g(x) đạt cực đại tại điểm \({{x}_{0}}\Leftrightarrow g'\left( {{x}_{0}} \right)=0\) và qua điểm \({{x}_{0}}\) thì g’(x) đổi dấu từ dương sang âm.
Lời giải chi tiết:
Ta có: \(g'\left( x \right)=f'\left( x \right)-1=0\Rightarrow f'\left( {{x}_{0}} \right)=1\Leftrightarrow \left[ \begin{align} & {{x}_{0}}=1 \\ & {{x}_{0}}=2 \\ & {{x}_{0}}=-1 \\ \end{align} \right.\)
\(\begin{align} & g'\left( x \right)>0\Leftrightarrow f'\left( x \right)>1\Leftrightarrow x\in \left( -\infty ;-1 \right)\cup \left( 2;+\infty \right) \\ & g'\left( x \right)<0\Leftrightarrow f'\left( x \right)<1\Leftrightarrow x\in \left( -1;1 \right)\cup \left( 1;2 \right) \\ \end{align}\)
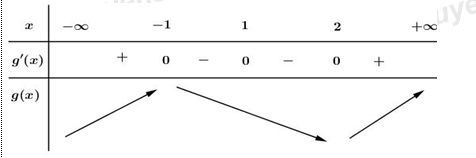
Ta có BBT:
Ta thấy qua \({{x}_{0}}=-1\) thì g’(x) đổi dấu từ dương sang âm, qua \({{x}_{0}}=1\) thì g’(x) không đổi dấu (luôn mang dấu âm) và qua \({{x}_{0}}=2\), g’(x) đổi dấu từ âm sang dương.
Vậy \({{x}_{0}}=-1\) là điểm cực đại của hàm số y = g(x).
Chọn D.