Phương pháp giải:

 Gọi \(H\) là trung điểm \(AB.\) chứng minh \(SH\) là đường cao. Áp dụng công thức \(V=\frac{1}{3}SH.{{S}_{ABCD}}\) để tính thể tích.

Lời giải chi tiết:

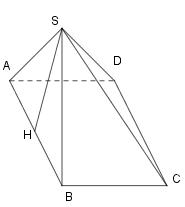
Gọi \(H\) là trung điểm \(\Delta SAB.\) Do \(\Delta SAB\) là tam giác đều nên \(SH\bot AB.\) Mặt khác theo giả thiết \(\left( SAB \right)\bot \left( ABCD \right)\) nên \(SH\bot \left( ABCD \right).\) Do đó \(SH\) là đường cao của \(S.ABCD.\) Do \(\Delta SAB\) là tam giác đều và \(ABCD\) là hình vuông cạnh \(a\sqrt{3}\) nên \(AB=SA=SB=a\sqrt{3}.\) Ta có \(H\) là trung điểm \(AB\) nên \(AH=\frac{AB}{2}=\frac{a\sqrt{3}}{2}.\) Áp dụng định lý Py-ta-go cho tam giác vuông \(SAH\) ta có \(HS=\sqrt{S{{A}^{2}}-A{{H}^{2}}}=\sqrt{{{\left( a\sqrt{3} \right)}^{2}}-{{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}}=\frac{3a}{2}.\) Do đó \(V=\frac{1}{3}SH.{{S}_{ABCD}}=\frac{1}{3}\left( \frac{3a}{2} \right){{\left( a\sqrt{3} \right)}^{2}}=\frac{3{{a}^{3}}}{2}.\)

Chọn đáp án B.