Phương pháp giải:

Chứng minh trung điểm của \(SC\) là tâm mặt cầu ngoại tiếp của chóp. Áp dụng định lý Py-ta-go để tìm bán kính mặt cầu ngoại tiếp.

Lời giải chi tiết:

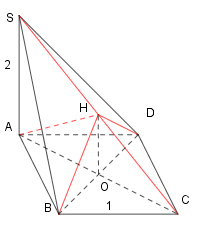
Áp dụng định lý Py-ta-go cho tam giác vuông \(ABC\) ta có \(AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=\sqrt{2}.\)

Do \(SA\bot \left( ABCD \right)\Rightarrow SA\bot AC.\) Áp dụng định lý Py-ta-go cho tam giác vuông \(SAC\) ta có \(SC=\sqrt{S{{A}^{2}}+A{{C}^{2}}}=\sqrt{{{2}^{2}}+{{\left( \sqrt{2} \right)}^{2}}}=\sqrt{6}.\)

Lấy \(H\) là trung điểm của \(SC.\) Khi đó do \(\Delta SAC\) vuông nên \(AH=HS=HC\,\,\left( 1 \right).\)

Giả sử \(O=AC\cap BD.\) Hạ \(HO.\) Khi đó tam giác \(\Delta HOB=\,\Delta HOD\,\,\left( c.c.c \right)\Rightarrow HB=HD\,\,\left( 2 \right).\) Ta lại có \(\left\{ \begin{array}{l}HO//SA\\SA \bot \left( {ABCD} \right)\end{array} \right. \Rightarrow HO \bot \left( {ABCD} \right) \Rightarrow \left\{ \begin{array}{l}HO \bot BD\\HO \bot AC.\end{array} \right.\)

Xét tam giác \(\Delta HOC,\Delta HOD.\) Ta có \(HO\) chung, \(OD=OC.\) \(\widehat{HOC}=\widehat{HOD}={{90}^{0}}.\) Do đó \(\Delta HOC=\Delta HOD\Rightarrow HC=DH\left( 3 \right).\)

Từ \(\left( 1 \right),\,\left( 2 \right),\left( 3 \right)\) ta có \(SH=HA=HB=HC=HD.\) Vậy \(H\) là tâm mặt cầu ngoại tiếp chóp. Khi đó bán kính là \(AH=\frac{1}{2}SC=\frac{\sqrt{6}}{2}.\) Thể tích của mặt cầu là \(V=\frac{4}{3}\pi .A{{C}^{3}}=\frac{4}{3}\pi .{{\left( \frac{\sqrt{6}}{2} \right)}^{3}}=\pi \sqrt{6}.\)

Chọn đáp án A.