Câu hỏi
Cho mặt cầu\(S\left( O;R \right)\)và mặt phẳng (P) cách (O) một khoảng \(\frac{R}{2}\) . Khi đó (P) cắt mặt cầu theo giao tuyến là một đường tròn có bán kính bằng:
- A \(\frac{R\sqrt{3}}{2}\)
- B \(\frac{2R\sqrt{3}}{2}\)
- C \(\frac{R}{2}\)
- D \(\frac{R\sqrt{3}}{4}\)
Phương pháp giải:
Xác định bán kính của thiết diện. Sau đó dùng định lý Py-ta-go để tính độ dài của bán kính.
Lời giải chi tiết:
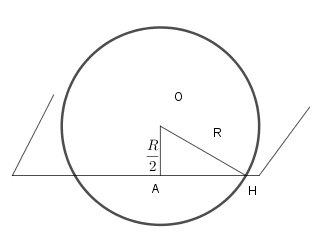
Bán kính của thiết diện chính là độ dài \(AH.\)
Áp dụng định lý Py-ta-go cho tam giác vuông
\(AOH\) ta có \(AH=\sqrt{O{{H}^{2}}-A{{O}^{2}}}=\sqrt{{{R}^{2}}-{{\left( \frac{R}{2} \right)}^{2}}}=\frac{R\sqrt{3}}{2}.\)
Chọn đáp án A.
Câu hỏi trước
