Câu hỏi
Hàm số \(\frac{ax+2}{x+b}\) có đồ thị như hình vẽ.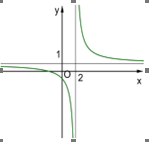
Khi đó giá trị của a và b là
- A \(a=1;b=2\)
- B \(a=b=1\)
- C \(a=1;b=-2\)
- D \(a=b=-2\)
Phương pháp giải:
Dùng định nghĩa của tiệm cận đứng, tiệm cận ngang để giải
Lời giải chi tiết:
Dựa vào đồ thị ta thấy đồ thị hàm số có tiệm cận đứng là \(x=2\) và tiệm cận ngang là \(y=1.\) Theo định nghĩa ta phải có \(\mathop {\lim }\limits_{x \to {2^ + }} y = \left[ \begin{array}{l}- \infty \\ + \infty \end{array} \right..\) Mặt khác \(\underset{x\to {{2}^{+}}}{\mathop{\lim }}\,y=\underset{x\to {{2}^{+}}}{\mathop{\lim }}\,\frac{ax+2}{x+b}.\)Do đó \(b=-2.\)
Với \(b=-2\) thì ta có \(\underset{x\to +\infty }{\mathop{\lim }}\,y=\underset{x\to +\infty }{\mathop{\lim }}\,\frac{ax+2}{x-2}=\underset{x\to +\infty }{\mathop{\lim }}\,\frac{a+\frac{2}{x}}{1-\frac{2}{x}}=a\Rightarrow a=1.\)
Chọn đáp án C.







