Câu hỏi
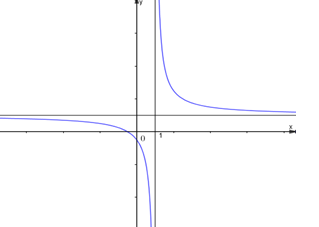
Đường cong ở hình bên là đồ thị hàm số \(y = {{ax + b} \over {cx + d}}\) , với a, b, c, d là các số thực. Mệnh đề nào dưới đây đúng?
- A \(y' > 0,\forall x \in R.\)
- B \(y' < 0,\forall x \in R.\)
- C \(y' > 0,\forall x \ne 1.\)
- D \(y' < 0,\forall x \ne 1.\)
Phương pháp giải:
Quan sát chiều của đồ thị hàm số và rút ra kết luận.
Lời giải chi tiết:
Ta có x = 1 là tiệm cận đứng của đồ thị hàm số nên TXĐ của hàm số là \(D = R\backslash \left\{ 1 \right\}\)
Hàm số liên tục trên \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\)
Theo chiều tăng của x, ta thấy đồ thị hàm số đi xuống trên toàn bộ TXĐ, tức là y giảm, do đó hàm số nghịch biến trên TXĐ của nó.
Chọn D.
Câu hỏi trước
