Phương pháp giải:

a)\(y = a{x^2} + bx + c\) có tọa độ đỉnh \(\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\)

Nếu a > 0 hàm số đồng biến trên \(\left( { - \frac{b}{{2a}}; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\)

Nếu a < 0 hàm số đồng biến trên \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\) và nghịch biến trên \(\left( { - \frac{b}{{2a}}; + \infty } \right)\) 

- Tìm giao điểm của đồ thị hàm số với các trục tọa độ.

- Vẽ đồ thị hàm số.

b) Giải phương trình hoành độ giao điểm.

Lời giải chi tiết:

a) TXĐ: D = R 

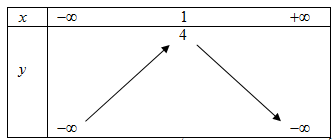
\( - \frac{b}{{2a}} = 1;\,\,\,y\left( { - \frac{b}{{2a}}} \right) = y\left( 1 \right) = 4\) Parabol có đỉnh  

\(a =  - 1 < 0\) nên hàm số đồng biến trên\(\left( { - \infty ;1} \right)\)và nghịch biến trên\(\left( {1; + \infty } \right)\)

Bảng Biến thiên:

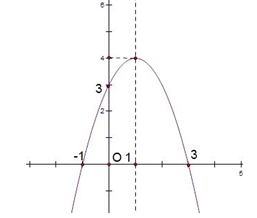
Đồ thị là parabol nhận I (1; 4) làm đỉnh, đường thẳng x = 1 làm trục đối xứng; cắt Ox tại hai điểm \(\left( { - 1;0} \right),\,\,\left( {3;0} \right)\) cắt Oy tại điểm (0; 3); đi qua điểm (2; 3)

(Lưu ý: học sinh cần phải xác định một số điểm quan trọng khi vẽ đồ thị)

b) Phương trình hoành độ giao điểm của hai đồ thị:

 \(- {x^2} + 2x + 3 = - 2x + 1 \Leftrightarrow {x^2} - 4x - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2 - \sqrt 6 \\x = 2 + \sqrt 6 \end{array} \right.\)

Có hai tọa độ giao điểm\(\left( {2 - \sqrt 6 ; - 3 + 2\sqrt 6 } \right),\,\,\,\left( {2 + \sqrt 6 ; - 3 - 2\sqrt 6 } \right)\)

Câu b chọn A