Câu hỏi
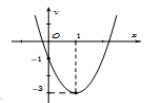
Cho parabol (P): \(y = a{x^2} + bx + c\) có đồ thị như hình bên. Phương trình của parabol này là:
- A \(y = 2{x^2} - 4x - 1\)
- B \(y = 2{x^2} + 3x - 1\)
- C \(y = 2{x^2} + 8x - 1\)
- D \(y = 2{x^2} - x - 1\)
Phương pháp giải:
Gọi Parabol cần tìm có dạng: \(y = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\), ta cần phải tìm ra ba ẩn a, b, c bằng cách lập 3 phương trình có chứa các biến a, b, c.
- Lập phương trình dựa vào tọa độ đỉnh và các điểm mà (P) đi qua.
Lời giải chi tiết:
Nhìn vào đồ thị hàm số ta thấy (P) có đỉnh \(I\left( {1; - 3} \right) \Rightarrow - \frac{b}{{2a}} = 1 \Leftrightarrow 2a + b = 0.\)
Vì \(I\left( {1, - 3} \right) \in \left( P \right) \Rightarrow - 3 = a + b + c\)
Ta có (P) đi qua điểm \(\left( {0; - 1} \right)\) nên ta có phương trình: \( - 1 = c\)
\( \Rightarrow \left\{ \begin{array}{l}2a + b = 0\\a + b + c = - 3\\c = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 4\\c = - 1\end{array} \right. \Rightarrow \left( P \right):y = 2{x^2} - 4x - 1.\)
Chọn A







