Câu hỏi
Cho hình hộp \(ABCD.{{A}^{'}}{{B}^{'}}{{C}^{'}}{{D}^{'}}\)có thể tích bằng V. E, F lần lượt là trung điểm của \(D{{D}^{'}}\) và \(C{{C}^{'}}\) . Khi đó ta có tỉ số \(\frac{{{V}_{EABD}}}{{{V}_{BCDEF}}}\) bằng
- A \(\frac{1}{2}\)
- B \(\frac{1}{3}\)
- C \(\frac{2}{3}\)
- D \(1\)
Phương pháp giải:
Chứng minh \({{V}_{BCDEF}}=2{{V}_{EABD}}.\)
Lời giải chi tiết:
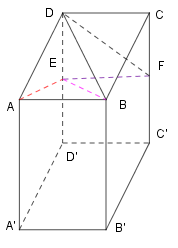
Ta có \(E,F\) là trung điểm của \(\text{DD}',\,CC'\) nên \(CF=DE=\frac{1}{2}CC'.\) Do đó \(\Delta ADE=\Delta BCF\,\,\left( c.g.c \right).\) Vì vậy \({{S}_{ADE}}={{S}_{BCF}}.\) Kéo theo
\({{V}_{EABD}}=\frac{1}{3}AB.{{S}_{ADE}}=\frac{1}{3}CD.{{S}_{BCF}}={{V}_{DBCF}}.\)
Tương tự ta có \({{S}_{BCF}}={{S}_{D\text{EF}}}\Rightarrow {{V}_{BCDF}}={{V}_{BDEF}}.\)
Từ đó \(\frac{{{V}_{EABD}}}{{{V}_{BCDEF}}}=\frac{{{V}_{EABD}}}{2{{V}_{EABD}}}=\frac{1}{2}.\)
Chọn đáp án A.
Câu hỏi trước
