Câu hỏi
Cho hình lăng trụ tam giác \(ABC.{{A}^{'}}{{B}^{'}}{{C}^{'}}\). Một đường thẳng đi qua trung điểm I của AB và song song với BC cắt AC tại J. Mặt phẳng \(\left( {{A}^{'}}IJ \right)\) chia khối lăng trụ thành 2 khổi. Tính tỉ số thể tích giữa hai khối đó (số bé chia cho số lớn).
- A \(\frac{1}{2}\)
- B \(\frac{1}{6}\)
- C \(\frac{1}{11}\)
- D \(\frac{1}{4}\)
Phương pháp giải:
So sánh thể tích \(A'\text{AIJ},A'B'C'CJIB\)
với thể tích của \(ABCA'B'C'.\)
Lời giải chi tiết:
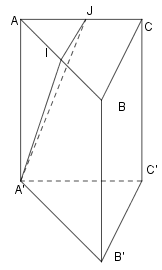
Ta có \(\text{IJ}\) là đường trung bình của \(\Delta ABC\) nên \(\text{IJ}=\frac{1}{2}BC.\)
Do đó \(d\left( A,\text{IJ} \right)=\frac{1}{2}d\left( A,BC \right).\) Kéo theo \({{S}_{\Delta ABC}}=\frac{1}{4}{{S}_{\Delta \text{AIJ}}}.\) Do \(A'\text{AIJ},\,ABCA'B'C'\) có cùng đường cao nên \({{V}_{ABCA'B'C'}}=12{{V}_{A'\text{AIJ}}}.\) Ta lại có \({{V}_{A'\text{AIJ}}}+{{V}_{A'B'C'CJIB}}={{V}_{ABCA'B'C'}}\) nên
\({{V}_{A'B'C'CJIB}}=\frac{11}{12}{{V}_{ABCA'B'C'}}.\)Do đó \(\frac{{{V}_{A'\text{AIJ}}}}{{{V}_{A'B'C'CJIB}}}=\frac{1}{11}.\)
Chọn đáp án C.







