Câu hỏi
Cho hình lập phương \(ABCD.{{A}^{'}}{{B}^{'}}{{C}^{'}}{{D}^{'}}\) cạnh a. Tính khoảng cách giữa đường thẳng AD và mặt phẳng \(\left( BC{{D}^{'}}{{A}^{'}} \right)\)?
- A \(\frac{a\sqrt{2}}{3}\)
- B \(a\)
- C \(a\sqrt{2}\)
- D \(\frac{a\sqrt{2}}{2}\)
Phương pháp giải:
Hạ đường cao \(DP\) xuống \(CD'.\) Khi đó \(DP\) chính là khoảng cách từ \(AD\) đến mặt phẳng \(\left( BCD'A' \right).\) Tính độ dài \(DP.\)
Lời giải chi tiết:
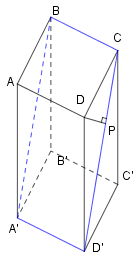
Hạ đường cao \(DP\) xuống \(CD'.\) Khi đó \(DP\) chính là khoảng cách từ \(AD\) đến mặt phẳng \(\left( BCD'A' \right).\)
Ta có \(DCD'\) là tam giác vuông cân tại \(D\) nên
\(C'D{{'}^{2}}=C{{D}^{2}}+D'{{D}^{2}}={{a}^{2}}+{{a}^{2}}=2{{a}^{2}}\Rightarrow C'D'=\sqrt{2}a.\)
Do \(\Delta DCD'\) là tam giác vuông cân nên \(DP\) vừa là đường cao vừa là trung tuyến, do đó
\(DP=\frac{1}{2}D'C=\frac{\sqrt{2}}{2}a.\) Vậy khoảng cách từ \(AD\) đến mặt phẳng \(\left( BCD'A' \right)\) là \(DP=\frac{\sqrt{2}}{2}a.\)
Chọn đáp án D.
Câu hỏi trước
