Phương pháp giải:

Xác định tâm mặt cầu ngoại tiếp chóp:

+ Tìm tâm O của đường tròn ngoại tiếp đa giác đáy

+ Dựng đường thẳng vuông góc với đáy và đi qua O

+ Tìm tâm mặt cầu ngoại tiếp là giao của d với một mặt phẳng trung trực của 1 cạnh bên

Lời giải chi tiết:

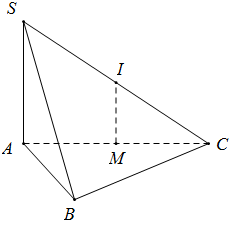
Gọi M, I lần lượt là trung điểm AC, SC

Có SA ⊥ (ABC), IM // SA ⇒ IM ⊥ (ABC)

∆ ABC vuông tại B ⇒ M là tâm đường tròn ngoại tiếp ∆ ABC

Mặt khác I thuộc mặt phẳng trung trực của SC ⇒ I là tâm mặt cầu ngoại tiếp hình chóp

Góc giữa SC và (ABC) là góc SCA = 45^o ⇒ ∆ SAC vuông cân tại A

Bán kính và thể tích mặt cầu ngoại tiếp hình chóp lần lượt là

\(\begin{array}{l}R = SI = \frac{{SC}}{2} = \frac{{AC\sqrt 2 }}{2} = \frac{{\sqrt 2 }}{2}\sqrt {A{B^2} + B{C^2}}  = \frac{{\sqrt 2 }}{2}\sqrt {{3^2} + {4^2}}  = \frac{{5\sqrt 2 }}{2}\\V = \frac{4}{3}\pi {R^3} = \frac{{125\pi \sqrt 2 }}{3}\end{array}\)

Chọn đáp án D