Phương pháp giải:

 Xác định tâm mặt cầu ngoại tiếp chóp:

+ Tìm tâm O của đường tròn ngoại tiếp đa giác đáy

+ Dựng đường thẳng vuông góc với đáy và đi qua O

+ Tìm tâm mặt cầu ngoại tiếp là giao của d với một mặt phẳng trung trực của 1 cạnh bên

Lời giải chi tiết:

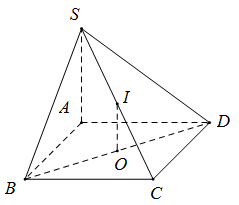
Gọi O là tâm đáy, I là trung điểm SC

Vì IO // SA ⇒ IO ⊥ (ABCD)

Mà I thuộc mặt phẳng trung trực của SC ⇒ I là tâm mặt cầu ngoại tiếp chóp. Bán kính mặt cầu này là

\(R=SI=\frac{SC}{2}=\frac{1}{2}\sqrt{S{{A}^{2}}+A{{C}^{2}}}=\frac{1}{2}\sqrt{S{{A}^{2}}+A{{B}^{2}}+B{{C}^{2}}}=\frac{1}{2}\sqrt{\left( 12{{a}^{2}} \right)+{{\left( 3a \right)}^{2}}+{{\left( 4a \right)}^{2}}}=\frac{13a}{2}\)

Chọn đáp án D