Câu hỏi
Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = a, CD = 2a. Góc giữa hai mặt phẳng (SBC) và (ABCD) bằng \({{60}^{\circ }}\) . Gọi I là trung điểm của AD. Biết hai mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng đáy. Thể tích của khối chóp S.ABCD là:
- A \({{V}_{S.ABCD}}=6{{a}^{3}}\sqrt{3}\)
- B \({{V}_{S.ABCD}}=\frac{6{{a}^{3}}\sqrt{15}}{5}\)
- C \({{V}_{S.ABCD}}=\frac{3{{a}^{3}}\sqrt{6}}{8}\)
- D \({{V}_{S.ABCD}}=6{{a}^{3}}\)
Phương pháp giải:
Xác định góc giứa (SBC) và đáy
Tính chiều cao hình chóp
Lời giải chi tiết:
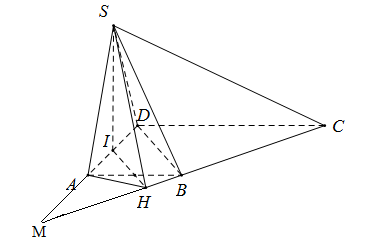
Gọi M là giao điểm của DA và CB.
Ta có:
\(\begin{array}{l}AB//CD \Rightarrow \dfrac{{AB}}{{CD}} = \dfrac{{MA}}{{MD}} = \dfrac{1}{2}\\\Rightarrow IA = ID = \dfrac{1}{4}MD \Rightarrow MI = \dfrac{3}{4}MD\\IH//BD \Rightarrow \dfrac{{MI}}{{MD}} = \dfrac{{IH}}{{BD}} = \dfrac{3}{4}\end{array}\)
Ta có SI ⊥ (ABCD)
Vẽ IH ⊥ BC tại H ⇒ BC ⊥ (SIH) ⇒ BC ⊥ SHGóc giữa (SBC) và (ABCD) là góc SHI = 60o
Ta chứng minh được ∆ BCD vuông cân tại B.
\(\begin{array}{l}IH = \dfrac{3}{4}BD = \dfrac{3}{4}AD\sqrt 2 = \dfrac{{3a\sqrt 2 }}{4}\\SI = IH.\tan 60^\circ = \dfrac{{3a\sqrt 6 }}{4}\\{S_{ABCD}} = \dfrac{1}{2}AD\left( {AB + CD} \right) = \dfrac{{3{a^2}}}{2}\\{V_{S.ABCD}} = \dfrac{1}{3}SI.{S_{ABCD}} = \dfrac{{3{a^3}\sqrt 6 }}{8}\end{array}\)
Chọn đáp án C







