Câu hỏi
Cho hình lập phương \(ABCD.{{A}^{'}}{{B}^{'}}{{C}^{'}}{{D}^{'}}\) . Gọi \(O,{{O}^{'}}\) lần lượt là tâm của hai hình vuông ABCD và \({{A}^{'}}{{B}^{'}}{{C}^{'}}{{D}^{'}}\) , \(O{{O}^{'}}=a\) .Gọi \({{V}_{1}}\) là thể tích khối trụ tròn xoay có đáy là hai đường tròn ngoại tiếp hình vuông ABCD và \({{A}^{'}}{{B}^{'}}{{C}^{'}}{{D}^{'}}\)và \({{V}_{2}}\) là thể tích khối nón tròn xoay đỉnh \({{O}^{'}}\)có đáy là đường tròn nội tiếp hình vuông ABCD. Tỉ số \(\frac{{{V}_{1}}}{{{V}_{2}}}\) là:
- A 2
- B 3
- C 4
- D 6
Phương pháp giải:
Tính thể tích của 2 khối tròn xoay và tính tỉ lệ
Lời giải chi tiết:
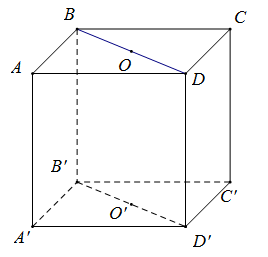
Ta có cạnh của hình lập phương là a
Khối trụ có đáy là 2 đường tròn ngoại tiếp 2 hình vuông thì có bán kính đáy \(R=OB=\frac{BD}{2}=\frac{a\sqrt{2}}{2}\) và chiều cao \(h=OO'=a\)
\({{V}_{1}}=\pi {{R}^{2}}h=\frac{\pi {{a}^{3}}}{2}\)
Khối nón đã cho có bán kính đáy \(r=\frac{a}{2}\) và chiều cao h nên
\(\begin{array}{l}{V_2} = \frac{1}{3}\pi {r^2}h = \frac{{\pi {a^3}}}{{12}}\\ \Rightarrow \frac{{{V_1}}}{{{V_2}}} = 6\end{array}\)
Chọn đáp án D







