Câu hỏi
Tìm tất cả các giá trị thực của tham số m để phương trình\(\left| {{x}^{4}}-2{{\text{x}}^{2}} \right|=m\) có 4 nghiệm phân biệt
- A \(m=1\).
- B \(m=0\).
- C \(-1<m<0\).
- D \(0<m<1\)
Phương pháp giải:
Tìm điều kiện để đồ thị hàm số y = x4 – 2x2 cắt đường thẳng y = m và đường thẳng y = –m tại tất cả 4 điểm phân biệt
Lời giải chi tiết:
Vẽ đồ thị hàm số \(y=x^4-2x^2\):
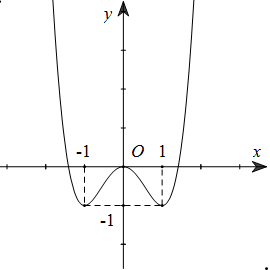
Từ đó ta suy ra đồ thị hàm số \(y = \left| {{x^4} - 2{x^2}} \right|\) như sau:
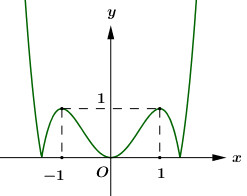
Dựa vào đồ thị hàm số ta thấy để phương trình ban đầu có 4 nghiệm phân biệt thì \(m=1\).
Chọn đáp án A.
Câu hỏi trước
