Câu hỏi
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại A. Biết SA vuông góc với mặt phẳng (ABC) và \(SA=1;AB=2,AC=3\). Tính bán kính r của mặt cầu đi qua các đỉnh A,B, C,S.
- A \(A=\sqrt{14}\).
- B \(A=2\sqrt{14}\).
- C \(4\).
- D \(A=\frac{\sqrt{14}}{2}\).
Phương pháp giải:
Tứ diện vuông (có 3 cạnh chung đỉnh đôi một vuông góc) và độ dài 3 cạnh đó là a, b, c thì có bán kính mặt cầu ngoại tiếp bằng \(R=\frac{1}{2}\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}\)
Lời giải chi tiết:
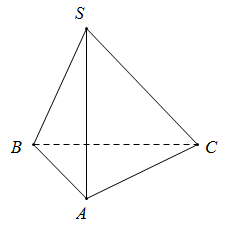
Mặt cầu đi qua 4 điểm A, B, C, S có bán kính \(R=\frac{1}{2}\sqrt{{{1}^{2}}+{{2}^{2}}+{{3}^{2}}}=\frac{\sqrt{14}}{2}\)
Chọn đáp án D
Câu hỏi trước
