Câu hỏi
Một tứ diện đều có độ dài mỗi cạnh là 2. Tính thể tích khối cầu ngoại tiếp tứ diện này.
- A \(\sqrt{6}\pi \).
- B \(2\sqrt{6}\pi \).
- C \(\frac{\sqrt{6}}{3}\pi \).
- D \(6\pi \).
Lời giải chi tiết:
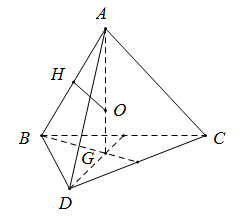
Xét tứ diện đều ABCD cạnh a
Gọi G là trọng tâm ∆ BCD
O là tâm mặt cầu ngoại tiếp tứ diện
Gọi H là trung điểm AB ⇒ OH ⊥ AB
\(\begin{array}{l}BG = \frac{{a\sqrt 3 }}{3}\\AG = \sqrt {A{B^2} - B{G^2}} = \frac{{a\sqrt 2 }}{{\sqrt 3 }}\\\Delta AHO\Delta AGB{\rm{ }}\left( {g.g} \right) \Rightarrow \frac{{AH}}{{AG}} = \frac{{AO}}{{AB}} \Rightarrow R = AO = \frac{{AH.AB}}{{AG}} = a\sqrt {\frac{3}{8}} \end{array}\)
Khối cầu ngoại tiếp tứ diện có thể tích \(V=\frac{4}{3}\pi {{R}^{3}}=\frac{\sqrt{6}}{8}\pi {{a}^{3}}\)
Thay a = 2 ta có \(V=\sqrt{6}\pi \)
Chọn đáp án A
Câu hỏi trước
