Câu hỏi
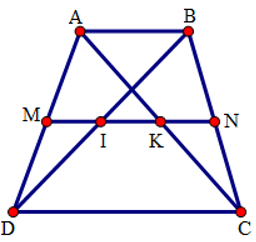
Cho hình thang \(ABCD\left( AB//CD \right)\), \(M\) là trung điểm của \(AD,\text{ }N\) là trung điểm của \(BC\) . Gọi \(I,\text{ }K\) theo thứ tự là giao điểm của \(MN\) với \(BD,\text{ }AC\) . Cho biết \(AB=6cm,CD=14cm\) . Tính các độ dài \(MI,\text{ }IK,\text{ }KN\).
- A \(\begin{array}{l}
MI = 3\,\,cm\\
IK = 4\,cm\\
KN = 3\,cm
\end{array}\) - B \(\begin{array}{l}
MI = 4\,\,cm\\
IK = 4\,cm\\
KN = 3\,cm
\end{array}\) - C \(\begin{array}{l}
MI = 3\,\,cm\\
IK = 4\,cm\\
KN = 4\,cm
\end{array}\) - D \(\begin{array}{l}
MI = 3\,\,cm\\
IK = 3\,cm\\
KN = 3\,cm
\end{array}\)
Phương pháp giải:
Sử dụng định lí đường trung bình của hình thang ta tính được \(MN\), sử dụng định lí đường trung bình của tam giác ta tính được \(MK,MI\).
Từ đó tính được \(IK,\text{ }KN\).
Lời giải chi tiết:
Xét hình thang \(ABCD\) có: \(M\) là trung điểm của \(AD;\text{ }N\) là trung điểm của \(BC\)
\(\Rightarrow \) \(MN\) là đường trung bình của hình thang \(ABCD\) \(\Rightarrow \left\{ \begin{align} & MN=\frac{AB+CD}{2}=\frac{6+14}{2}=10(cm) \\ & MN//AB//CD \\\end{align} \right.\)
Xét \(\Delta ADC\) có: \(AM\text{ }=\text{ }MD,\text{ }MK\text{ }//\text{ }DC\) nên \(AK=KC\) (định lí đường trung bình của tam giác)
\(\Rightarrow \)\(MK\) là đường trung bình của \(\Delta ADC\Rightarrow MK=\frac{DC}{2}=\frac{14}{2}=7\left( cm \right)\)
Xét \(\Delta ABD\) có: \(AM\text{ }=\text{ }MD,\text{ }MI\text{ }//\text{ }AB\) nên \(BI=ID\) (định lí đường trung bình của tam giác)
\(\Rightarrow \) \(MI\) là đường trung bình của \(\Delta ABD\Rightarrow MI=\frac{AB}{2}=\frac{6}{2}=3\left( cm \right)\)
\(\begin{align} & \Rightarrow IK=MK-MI=7-3=4\,(cm) \\ & KN=MN-MK=10-7=3\,(cm) \\\end{align}\)