Phương pháp giải:

Ta đi chứng minh đường trung bình của hình thang cân \(ABCD\) bằng đường cao đi qua giao điểm của hai đường chéo của hình thang

Sử dụng định lí đường trung bình của hình thang để tính

Lời giải chi tiết:

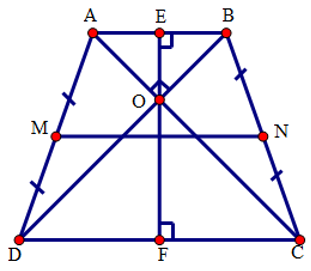
Xét hình thang cân \(ABCD\left( AB//CD \right)\) , hai đường chéo \(AC\) và \(BD\) vuông góc với nhau tại \(O,\text{ }MN\) là đường trung bình của hình thang \(ABCD.\)

Qua \(O\) kẻ đường thẳng vuông góc với \(AB\) tại \(E,\)  với \(CD\) tại \(F.\) 

Xét \(\Delta ADC\) và \(\Delta BCD\) có:

\(AD=BC\) (gt)

DC cạnh chung

\(\widehat{ADC}=\widehat{BCD}\) (gt)

\(\Rightarrow \Delta ADC=\Delta BCD(c.g.c)\Rightarrow \widehat{ACD}=\widehat{BDC}\) (hai góc tương ứng)

\(\Rightarrow \Delta OCD\) cân tại \(O \)

\(\Rightarrow OC=OD\) (tính chất tam giác cân).

Mà \(AC=BD\) nên \(OA=OB\Rightarrow \Delta OAB\) cân tại \(O\).

Lại có \(\widehat{AOB}=90{}^\circ \) (do \(AB\) vuông góc với \(CD\)) nên \(\Delta AOB\) vuông cân tại \(O\) nên  \(OE=\frac{AB}{2}\).

Tương tự: tam giác \(DOC\) vuông cân tại \(O\) nên \(FO=\frac{CD}{2}\)

Do đó \(FE=\frac{AB+CD}{2}\)

\(MN\) là đường trung bình của hình thang \(ABCD\) nên \(MN=\frac{AB+CD}{2}\)

\(\Rightarrow MN=FE=10cm\)