Câu hỏi
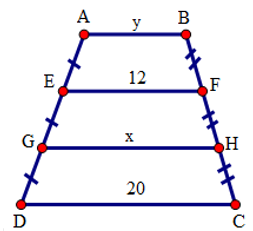
Tìm \(x,\text{ }y\) trên hình vẽ, trong đó \(AB//EF//GH//CD\).
- A \(x=14cm,\,y=7cm\)
- B \(x=8cm,\,y=16cm\)
- C \(x=16cm,\,y=8cm\)
- D \(x=7cm,\,y=14cm\)
Phương pháp giải:
Sử dụng định lí đường trung bình của hình thang
Lời giải chi tiết:
Vì \(EF//DC\) nên \(EFCD\) là hình thang.
Lại có: \(GE=GD,FH=HC\) nên \(GH\) là đường trung bình của hình thang \(EFCD\)
\(\Rightarrow GH=\frac{CD+EF}{2}=\frac{20+12}{2}=16(cm)=x\)
Vì \(AB//GH\) nên \(ABHG\) là hình thang.
Lại có: \(GE=EA,FH=BF\) nên \(EF\) là đường trung bình của hình thang \(ABHG\)
\(\Rightarrow EF=\frac{AB+GH}{2}\Leftrightarrow 12=\frac{y+16}{2}\Leftrightarrow y=8(cm)\) .
Vậy \(x=16cm,\,y=8cm\).