Câu hỏi
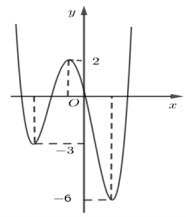
Hình vẽ là đồ thị hàm số \(y = f\left( x \right)\). Gọi \(S\) là tập hợp các giá trị nguyên dương của tham số m để hàm số \(y = \left| {f\left( {x-1} \right) + m} \right|\) có \(5\) điểm cực trị. Tổng giá trị tất cả các phần tử của \(S\) bằng
- A \(9\)
- B \(12\)
- C \(18\)
- D \(15\)
Phương pháp giải:
Phương pháp:
+ Xác định đồ thị hàm số \(y = f\left( {x-1} \right)\)
+ Áp dụng tính chất: Số cực trị của đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) bằng tổng số cực trị của đồ thị hàm số \(y = f\left( x \right)\) và số giao điểm (không phải là cực trị) của đồ thị hàm số \(y = f\left( x \right)\) với \(Ox\)
Lời giải chi tiết:
Cách giải
Tịnh tiến đồ thị hàm số \(y = f\left( x \right)\) sang phải \(1\) đơn vị, ta được đồ thị hàm số \(y = f\left( {x-1} \right)\)
Do đó đồ thị hàm số \(y = f\left( {x-1} \right)\) có \(3\) cực trị và có \(4\) giao điểm với \(Ox\).
Để được đồ thị hàm số \(y = f\left( {x-1} \right) + m\) với \(m\) nguyên dương ta phải tịnh tiến đồ thị hàm số \(y = f\left( {x-1} \right)\) lên trên \(m\) đơn vị
Để thỏa mãn điều kiện đề bài thì đồ thị hàm số \(y = f\left( {x-1} \right) + m\) cắt \(Ox\) tại đúng \(2\) điểm (không phải là điểm cực trị của chính nó), do đó \(3 \leqslant m < 6\)
\( \Rightarrow S = \left\{ {3;4;5} \right\}\)
Tổng giá trị các phần tử của \(S\) là \(12\).
Chọn đáp án B







