Phương pháp giải:

Phương pháp: Sử dụng thể tích phần bù: Chia thể tích chóp \(S.ABCD\) thành nhiều phần và tính thể tích các phần còn lại, sau đó lấy thể tích chóp trừ đi.

Lời giải chi tiết:

Cách giải

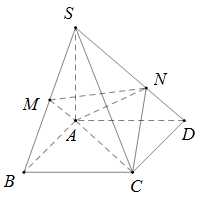
Ta có

\(\begin{array}{l}{V_{MABC}} = \dfrac{1}{2}{V_{SABC}} = \dfrac{1}{4}{V_{S.ABCD}}\\{V_{NACD}} = \dfrac{1}{3}{V_{SACD}} = \dfrac{1}{6}{V_{S.ABCD}}\\\dfrac{{{V_{SMAN}}}}{{{V_{SBAD}}}} = \dfrac{{{V_{SMCN}}}}{{{V_{SBCD}}}} = \dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SD}} = \dfrac{1}{2}.\dfrac{2}{3} = \dfrac{1}{3}\\ \Rightarrow {V_{SMAN}} = {V_{SMCN}} = \dfrac{1}{3}.\dfrac{1}{2}{V_{S.ABCD}} = \dfrac{1}{6}{V_{S.ABCD}}\\ \Rightarrow {V_{ACMN}} = {V_{S.ABCD}} - {V_{MABC}} - {V_{NACD}} - {V_{SMAN}} - {V_{SMCN}} = \dfrac{1}{4}{V_{S.ABCD}}\\ = \dfrac{1}{4}.\dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{{12}}.a.{a^2} = \dfrac{{{a^3}}}{{12}}\end{array}\)

Chọn đáp án A