Câu hỏi
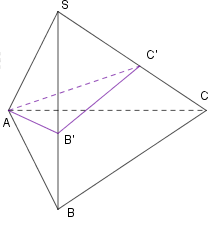
Cho khối chóp \(S.ABC\) có \(\widehat{ASB}=\widehat{BSC}=\widehat{CSA}={{60}^{0}},SA=a,SB=2a,SC=4a.\) Tính thể tích khối chóp \(S.ABC\) theo \(a.\)
- A \(\frac{8{{a}^{3}}\sqrt{2}}{3}.\)
- B \(\frac{2{{a}^{3}}\sqrt{2}}{3}.\)
- C \(\frac{4{{a}^{3}}\sqrt{2}}{3}.\)
- D \(\frac{{{a}^{3}}\sqrt{2}}{3}.\)
Phương pháp giải:
Phương pháp. Tính \({{V}_{S.AB'C'}}.\) Sử dụng công thức \(\frac{{{V}_{S.AB'C'}}}{{{V}_{S.ABC}}}=\frac{SA}{SA}.\frac{SB'}{SB}.\frac{SC'}{SC}=\frac{SB'}{SB}.\frac{SC'}{SC}\)để suy ra \({{V}_{S.ABC.}}\)
Lời giải chi tiết:
Lời giải chi tiết.
Gọi \(B',\,C'\) lần lượt là điểm thuộc \(SB,SC\) sao cho \(SB'=SC'=a.\)
Ta có \(\widehat{ASB}=\widehat{BSC}=\widehat{CSA}={{60}^{0}},SA=SB=SC=a\) nên \(S.AB'C'\) là tứ diện
đều cạnh \(a.\) Do đó thể tích của tứ diện này là \({{V}_{S.AB'C'}}=\frac{{{a}^{3}}\sqrt{2}}{12}.\)
Ta có
\(\frac{{{V}_{S.AB'C'}}}{{{V}_{S.ABC}}}=\frac{SB'}{SB}.\frac{SC'}{SC}=\frac{a}{2a}.\frac{a}{4a}=\frac{1}{8}\Rightarrow {{V}_{S.ABC}}=8{{V}_{S.AB'C'}}=8.\frac{{{a}^{3}}\sqrt{2}}{12}=\frac{2{{a}^{3}}\sqrt{2}}{3}.\)
Chọn đáp án B.