Câu hỏi
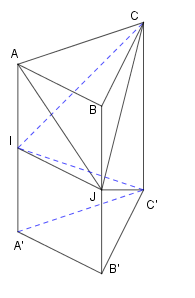
Cho khối lăng trụ tam giác \(ABC.A'B'C'\) có thể tích là \(V.\) Gọi \(I,J\) lần lượt là trung điểm hai cạnh \(AA'\) và \(BB'.\) Khi đó thể tích của khối đa diện \(ABCIJC'\) bằng.
- A \(\frac{4}{5}V.\)
- B \(\frac{3}{4}V.\)
- C \(\frac{5}{6}V.\)
- D \(\frac{2}{3}V.\)
Phương pháp giải:
Phương pháp. Chứng minh \({{V}_{ABCIJ}}={{V}_{A'B'C'IJ}}=2{{V}_{AIJC}},{{V}_{JICC'}}=2{{V}_{JAIC}}.\)Từ đó suy ra \(V_{ABCIJC'}.\)
Lời giải chi tiết:
Lời giải chi tiết.
Vì \(I,J\) là trung điểm của \(AA',BB'\) nên \({{V}_{ABCIJ}}={{V}_{A'B'C'IJ}}=2{{V}_{AIJC}}.\)
Vì \({{S}_{\Delta ICC'}}=2{{S}_{\Delta AIC}}\Rightarrow {{V}_{JICC'}}=2{{V}_{JAIC}}.\)
Mà \({V_{ABCA'B'C'}} = {V_{ABCIJ}} + {V_{A'B'C'IJ}} + {V_{JICC'}}\)\( \Rightarrow \)\({V_{ABCIJ}} = \frac{1}{3}V\)\( \Rightarrow \)\({V_{ABCIJC'}} = \frac{2}{3}V\)
Chọn đáp án D.
Câu hỏi trước
