Câu hỏi
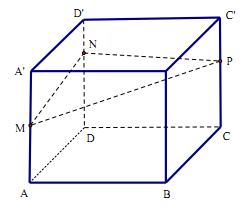
Cho khối hộp chữ nhật \(ABCD.A'B'C'D'\) có thể tích bằng \(2110\) . Biết \(A'M = MA;DN = 3ND';CP = 2PC'\) như hình vẽ. Mặt phẳng \(\left( {MNP} \right)\) chia khối hộp đã cho thành hai khối đa diện. Thể tích khối đa diện nhỏ hơn bằng
- A \(\dfrac{{7385}}{{18}}\)
- B \(\dfrac{{5275}}{{12}}\)
- C \(\dfrac{{8440}}{9}\)
- D \(\dfrac{{5275}}{6}\)
Phương pháp giải:
Phương pháp: Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có thể tích \(V\). Một mặt phẳng cắt các đoạn \(AA',BB',CC',DD'\) theo thứ tự tại \(M,N,P,Q\) thì thể tích \(V'\) của khối đa diện \(ABCD.MNPQ\) được tính theo công thức: \(V' = \dfrac{V}{2}\left( {\dfrac{{AM}}{{AA'}} + \dfrac{{CP}}{{CC'}}} \right) = \dfrac{V}{2}\left( {\dfrac{{BN}}{{BB'}} + \dfrac{{DQ}}{{DD'}}} \right)\)
Lời giải chi tiết:
Cách giải
Thể tích của khối đa diện nhỏ hơn là \(V = \dfrac{{{V_{ABCD.A'B'C'D'}}}}{2}\left( {\dfrac{{AM}}{{AA'}} + \dfrac{{CP}}{{CC'}}} \right) = \dfrac{{2110}}{2}.\left( {\dfrac{1}{2} + \dfrac{1}{3}} \right) = \dfrac{{5275}}{6}\)
Chọn đáp án D







