Câu hỏi
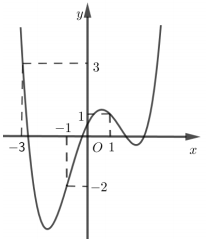
Cho hàm số \(y = f\left( x \right)\) có đồ thị \(y = f'\left( x \right)\) ở hình vẽ. Xét hàm số
\(g\left( x \right) = f\left( x \right) - \dfrac{1}{3}{x^3} - \dfrac{3}{4}{x^2} + \dfrac{3}{2}x + 2018\), mệnh đề nào dưới đây đúng?
- A \(\mathop {\min }\limits_{\left[ { - 3;1} \right]} g\left( x \right) = g\left( { - 3} \right)\)
- B \(\mathop {\min }\limits_{\left[ { - 3;1} \right]} g\left( x \right) = g\left( { - 1} \right)\)
- C \(\mathop {\min }\limits_{\left[ { - 3;1} \right]} g\left( x \right) = g\left( 1 \right)\)
- D \(\mathop {\min }\limits_{\left[ { - 3;1} \right]} g\left( x \right) = \dfrac{{g\left( { - 3} \right) + g\left( 1 \right)}}{2}\)
Phương pháp giải:
Phương pháp: Lập bảng biến thiên của \(g\left( x \right)\) dựa vào bảng xét dấu \(g'\left( x \right)\)
Lời giải chi tiết:
Cách giải
Ta có \(g'\left( x \right) = f'\left( x \right) - {x^2} - \dfrac{3}{2}x + \dfrac{3}{2} = f'\left( x \right) - \left( {{x^2} + \dfrac{3}{2}x - \dfrac{3}{2}} \right)\)
Đồ thị hàm số \(y = h\left( x \right) = {x^2} + \dfrac{3}{2}x - \dfrac{3}{2}\) như hình bên
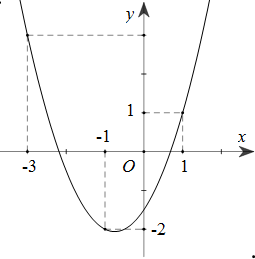
Trong đoạn \(\left[ {-3;1} \right]\) , ta có
\(\begin{array}{l}g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = h\left( x \right) = {x^2} + \dfrac{3}{2}x - \dfrac{3}{2} \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = \pm 1\end{array} \right.\\g'\left( x \right) > 0 \Leftrightarrow f'\left( x \right) > h\left( x \right) \Leftrightarrow - 1 < x < 1\\g'\left( x \right) < 0 \Leftrightarrow f'\left( x \right) < h\left( x \right) \Leftrightarrow - 3 < x < - 1\end{array}\)
Ta có bảng biến thiên:
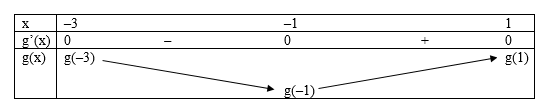
Từ bảng biến thiên ta có \(\mathop {\min }\limits_{\left[ { - 3;1} \right]} g\left( x \right) = g\left( { - 1} \right)\)
Chọn đáp án B







