Câu hỏi
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, cạnh bên \(SA\) vuông góc với đáy. Biết khoảng cách từ \(A\) đến \(\left( {SBD} \right)\) bằng \(\dfrac{{6a}}{7}\). Khoảng cách từ điểm \(C\) đến mặt phẳng \(\left( {SBD} \right)\) bằng
- A \(\dfrac{{6a}}{7}\)
- B \(\dfrac{{12a}}{7}\)
- C \(\dfrac{{3a}}{7}\)
- D \(\dfrac{{4a}}{7}\)
Phương pháp giải:
Phương pháp: Xét \(A,B,C,D\) là \(4\) điểm đồng phẳng. Khi khoảng cách từ \(A\) và \(C\) đến đường thẳng \(BD\) bằng nhau thì khoảng cách từ \(A\) và \(C\) đến mặt phẳng \(\left( {SBD} \right)\) cũng bằng nhau
Lời giải chi tiết:
Cách giải
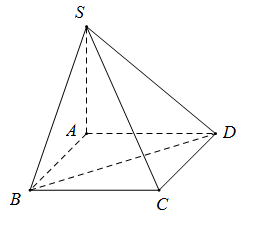
Khoảng cách từ \(C\) đến \(\left( {SBD} \right)\) cũng bằng
\(d\left( {C;\left( {SBD} \right)} \right) = d\left( {A;\left( {SBD} \right)} \right) = \dfrac{{6a}}{7}\)
Chọn đáp án A
Câu hỏi trước
