Câu hỏi
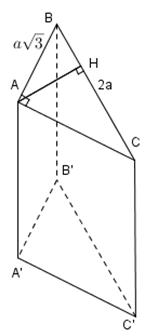
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác \(ABC\) vuông tại \(A\) có \(BC=2a,\,AB=a\sqrt{3}.\) Khoảng cách từ \(AA'\) đến mặt phẳng \(\left( BCC'B' \right)\) là:
- A \(\frac{a\sqrt{21}}{7}.\)
- B \(\frac{a\sqrt{3}}{2}.\)
- C \(\frac{a\sqrt{5}}{2}.\)
- D \(\frac{a\sqrt{7}}{3}.\)
Phương pháp giải:
Hạ đường cao \(AH\) xuống cạnh \(BC.\) Khi đó khoảng cách từ \(AA'\)
đến \(\left( BCC'B' \right)\) chính là độ dài \(AH.\) Áp dụng định lý Py-ta-go và hệ thức
trong tam giác vuông \(ABC\) để tìm \(AH.\)
Lời giải chi tiết:
Hạ đường cao \(AH\) xuống cạnh \(BC.\) Khi đó khoảng cách từ \(AA'\)
đến \(\left( BCC'B' \right)\) chính là độ dài \(AH.\) Ta có \(\Delta ABC\) vuông tại \(A\) nên
theo định lý Py-ta-go ta nhận được \(A{{C}^{2}}=B{{C}^{2}}-A{{B}^{2}}={{\left( 2a \right)}^{2}}-{{\left( a\sqrt{3} \right)}^{2}}={{a}^{2}}\Rightarrow AC=a.\)
Áp dụng hệ thức trong
tam giác vuông\(ABC\) ta nhận được
\(\dfrac{1}{A{{H}^{2}}}=\dfrac{1}{A{{B}^{2}}}+\dfrac{1}{A{{C}^{2}}}=\dfrac{1}{{{\left( a\sqrt{3} \right)}^{2}}}+\dfrac{1}{{{a}^{2}}}=\dfrac{4}{3{{a}^{2}}}\Rightarrow AH=\dfrac{\sqrt{3}a}{2}.\)
Chọn đáp án B.