Câu hỏi
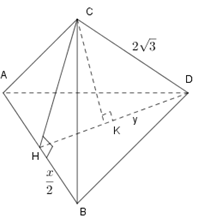
Xét khối tứ diện \(ABCD,\,AB=x,\) các cạnh còn lại bằng \(2\sqrt{3}.\) Tìm \(x\) để thể tích khối tứ diện \(ABCD\) lớn nhất.
- A \(x=\sqrt{6}.\)
- B \(x=2\sqrt{2}.\)
- C \(x=\sqrt{14}.\)
- D \(x=3\sqrt{2}.\)
Phương pháp giải:
Phương pháp.Gọi \(H\)là trung điểm của cạnh \(AB.\)Hạ đường cao \(CK\) xuống \(HD.\)Vậy \(CK\) là đường cao của tứ diện. Áp dụng định lý Py-ta-go để tính \(CK.\) Sử dụng công thức tính thể tích để tính thể tích tứ diện. Áp dụng bất đẳng thức Cô-si để tìm giá trị lớn nhất của tứ diện.
Lời giải chi tiết:
Lời giải chi tiết.
Gọi \(H\) là trung điểm của cạnh \(AB,\) do \(\Delta ABC\) cân tại \(C\) nên \(CH\) là đường cao. Tam giác \(ABD\) có \(AD=DB=2\sqrt{3}\) nên là tam giác cân tại \(D.\)Do đó \(HD\)là đường cao. Khi đó ta có
\(\left\{ \begin{align}& CH\bot AB \\& HD\bot AB \\\end{align} \right.\Rightarrow AB\bot \left( CHD \right).\)
Hạ đường cao \(CK\)xuống \(HD\) khi đó \(CK\bot AB.\) Do đó \(CK\bot \left( ABD \right).\) Vậy \(CK\) là đường cao của tứ diện.
Ta có \(HB=\frac{x}{2}.\) Áp dụng định lý Py-ta-go cho tam giác \(HBC\) ta có
\(HC=\sqrt{B{{C}^{2}}-H{{B}^{2}}}=\sqrt{{{\left( 2\sqrt{3} \right)}^{2}}-{{\left( \frac{x}{2} \right)}^{2}}}=\frac{\sqrt{48-{{x}^{2}}}}{2}.\)
Tương tự ta có \(HD=\frac{\sqrt{48-{{x}^{2}}}}{2}.\)Đặt \(y=KD.\)
Áp dụng định lý Py-ta-go cho tam giác \(CHK\) và \(CKD\) ta có
\(\begin{align}& \,\,\,\,\,\,\,C{{K}^{2}}=C{{H}^{2}}-H{{K}^{2}}=C{{D}^{2}}-K{{D}^{2}}\Leftrightarrow C{{H}^{2}}-{{\left( HD-y \right)}^{2}}={{\left( 2\sqrt{3} \right)}^{2}}-{{y}^{2}} \\& \Leftrightarrow C{{H}^{2}}-H{{D}^{2}}+2HD.y-{{y}^{2}}=12-{{y}^{2}}\Leftrightarrow 2HD.y=12\Leftrightarrow y=\frac{6}{HD}=\frac{12}{\sqrt{48-{{x}^{2}}}}. \\\end{align}\)
Vì vậy \(C{{K}^{2}}=C{{D}^{2}}-{{y}^{2}}=12-{{\left( \frac{12}{\sqrt{48-{{x}^{2}}}} \right)}^{2}}=\frac{12\left[ \left( 48-{{x}^{2}} \right)-12 \right]}{48-{{x}^{2}}}=\frac{12\left( 36-{{x}^{2}} \right)}{48-{{x}^{2}}}\Rightarrow CK=\sqrt{\frac{12\left( 36-{{x}^{2}} \right)}{48-{{x}^{2}}}}.\)
Diện tích tam giác \(ABD\) là \({{S}_{1}}=\frac{1}{2}AB.HD=\frac{1}{2}x\frac{\sqrt{48-{{x}^{2}}}}{2}=\frac{x\sqrt{48-{{x}^{2}}}}{4}.\)
Do đó thể tích tứ diện là \(V=\frac{1}{3}CK.{{S}_{1}}=\frac{1}{3}.\sqrt{\frac{12\left( 36-{{x}^{2}} \right)}{48-{{x}^{2}}}}.\frac{x\sqrt{48-{{x}^{2}}}}{4}=\frac{1}{6}\sqrt{3}.x\sqrt{36-{{x}^{2}}}.\)
Áp dụng bất đẳng thức Cô-si cho \(\left( x,\sqrt{36-{{x}^{2}}} \right)\) ta có
\(V=\frac{\sqrt{3}}{6}x\sqrt{36-{{x}^{2}}}\le \frac{\sqrt{3}}{6}\frac{{{x}^{2}}+\left( 36-{{x}^{2}} \right)}{2}=3\sqrt{3}.\)
Dấu bằng xảy ra khi và chỉ khi \(x=\sqrt{36-{{x}^{2}}}\Leftrightarrow x=\sqrt{18}=3\sqrt{2}.\)
Chọn đáp án D.